Hilbert–Samuel function

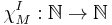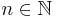In commutative algebra the Hilbert–Samuel function, named after David Hilbert and Pierre Samuel,^[1] of a nonzero finitely generated module $M$ over a commutative Noetherian local ring $A$ and a primary ideal $I$ of $A$ is the map $\chi_{M}^{I}:\mathbb{N}\rightarrow\mathbb{N}$ such that, for all $n\in\mathbb{N}$ ,

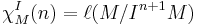
$\chi_{M}^{I}(n)=\ell(M/I^{n%2B1}M)$

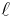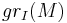where $\ell$ denotes the length over $A$ . It is related to the Hilbert function of the associated graded module $gr_I(M)$ by the identity

$\chi_M^I (n)=\sum_{i=0}^n H(gr_I(M),i),$

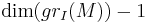For sufficiently large $n$ , it coincides with a polynomial function of degree equal to $\dim(gr_I(M))-1$ .^[2]

Examples

For the ring of formal power series in two variables $k[[x,y]]$ taken as a module over itself and graded by the order and the ideal generated by the monomials x² and y³ we have

$\chi(1)=1,\quad \chi(2)=3,\quad \chi(3)=5,\quad \chi(4)=6\text{ and } \chi(k)=6\text{ for }k > 4.$ ^[3]

References

^ H. Hironaka, Resolution of Singularities of an Algebraic Variety Over a Field of Characteristic Zero: I. Ann. of Math. 2nd Ser., Vol. 79, No. 1. (Jan., 1964), pp. 109-203.
^ Atiyah, M. F. and MacDonald, I. G. Introduction to Commutative Algebra. Reading, MA: Addison–Wesley, 1969.
^ Ibidem